Exponential Functions and Equations
Including Growth and Decay

The math form f(x) = ax defines Exponential Functions of base a if a is a positive real number. Its domain is all real numbers and its range is all positive real numbers.

An equation or function having exponential form is often first identified by its variable exponent.

Though not Polynomial, Exponential Equations are sometimes referenced as a Non-constant Polynomial.

Equation examples:

y = 3x

y = 7x−2

y = ex

y = (1/3)−x

Solving Exponential Equations

By providing a value of x and computing the resulting y value solves an exponential equation. The following are x and y values for two separate equations:

x    y = 3x

4   81

3   27

2     9

1     3

0     1

−1  1/3

−2  1/9

−3  1/27

−4  1/81

x    y = 10x

4   10000

3     1000

2       100

1         10

0           1

−1  1/10

−2  1/100

−3  1/1000

−4  1/10000

Exponential Graph

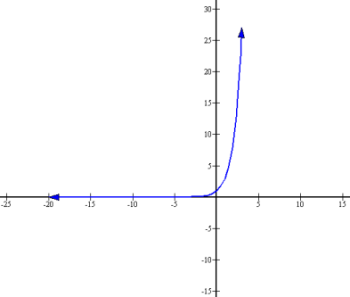
Graph of y = 3x

The graph line approaches but never reaches the x axis. The x axis is a horizontal asymptote.

There is no value of x that will make 3x equal 0 or a negative number, a property of all exponential math functions.

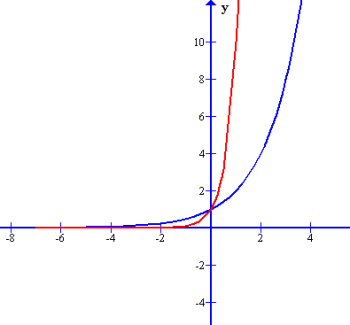
Comparing the Graph of y = 3x and y = 10x

The graph of a base that is greater than 1 has positive slope, a base less than 1 has negative slope, another property of all exponential functions.

The equation y = (1/2)x has a base less than 1 and a negative sloping graph:

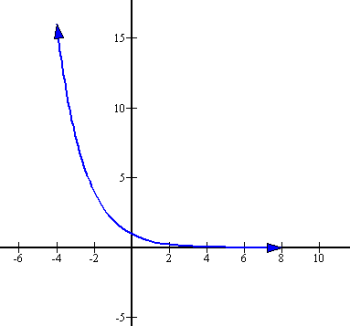
Graph of y = (1/2)x

Logarithms are inverse functions of Exponential Equations:

Exponential Growth Formula

y = ex is a special function that occurs frequently in economics and biological growth. e is an irrational number (of approximate value 2.71828…) and is the Natural Logarithm. A complete definition of e requires calculus.

e is basic to the study of Statistics and appears in the Normal Probability Density Function.

The growth curve of a population of insects in biology has the equation:

y = P0eh(t − t0)

P0 is the population size at time t0. h is a constant depending on the type of population, and y is the population size at any instant t. When this equation applies it means y increases according to the Exponential Growth Law.

The Exponential Growth Formula assumes optimal or ideal conditions. In biology it does not consider pollutants, weather, insufficient nutrition or other criteria that could negatively impact a studied population growth.

Exponential Growth graphs are positive sloping.

Exponential Decay

Almost always Exponential Decay refers is a radioactive element of decreasing mass.

The number of atoms, y, of a radioactive element can be defined at an instant in time as:

y = W0e−h(t − t0)

e has approximate value 2.71828…

W0 is the number of atoms at time t0 and h depends on the element. When the equation applies it means y is decreasing according to the Exponential Law of Decay.

Exponential Decay has a negative exponent. It means that e can be written as a denominator:

y =

W0

eh(t − t0)

Copyright © DigitMath.com

All Rights Reserved.