The Math We Need

Math evolved not as a science, but as individual solutions to simplify difficult problems that occur often, as methods to improve efficiency. It is often described as our study of measurements, properties and relationships of quantities. We do this by counting, comparing and organizing.

Both spoken and written, math provides us a language that helps describe and document the behavior of objects, items and ideas using measurements, properties and relationships of quantities.

Math has rules and methods, unique numerals and symbols, each has specific meaning.

Some examples help us understand our need for math…

Some of our still widely applied mathematics were founded thousands of years ago. Ancient civilizations dealt with creating structure, cities and buildings, and being able to control the process of many people working together to complete a construction over many years within a fixed cost. These are problems that we face today.

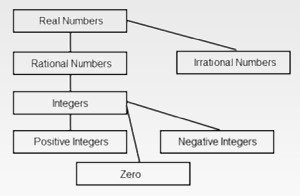
The domain of most mathematics is Real Numbers:

Most of us use Rational Numbers every day.

… and Irrational Numbers including pi, e, square root and logarithm when their value cannot be written as the ratio of two integers.

Mathematics relates to other subjects like science, accounting, engineering, art, and music. These subjects and many others depend on math for at least one of the following:

Patterns and Relationships: Patterns are things that repeat forming relationships of physical objects or concepts that are connected.

Geometry and Spatial Sense: Geometry involves shape, size, space, position, direction, and movement. It describes and classifies the physical world.

Measurement: Measurement assigns length, width and weight to an object using standard units like inches, feet, and pounds. Time is measured using hours, seconds, and minutes.

Estimating: To estimate is to approximate the amount or size of something.

 Statistics and probability: Using graphs and charts to organize and interpret data into relationships to form meaningful information.

The Roman Colosseum, 80 AD, is an amphitheater seating 50,000 to 80,000 persons, was built without modern day electric or engine powered machinery in just 10 years.

It has a ground area of 6 acres, required 3,531,467 cubic feet of travertine stone and 300 tons of iron clamps.

 Applied mathematics described the Colosseum to communicate exact dimensions for massive stone blocks and columns quarried and cut over 20 miles from the construction site. The quarry was near what today is Tivoli. As stone blocks and columns arrived to the construction site they fit together exactly and concrete was only used with arch stones.

Geometrical patterns we have created exist everywhere, their symmetry provide beauty and a sense of purpose.

The Empire State Building is 1,454 feet high. Its 102 floors, on average, accommodate 21,000 persons each day.

Using engineering techniques incorporating advanced mathematics the Empire State Building was completed in just 410 days, less than the expected 18 months. It opened on May 1, 1931.

A just-in-time construction project. Its steel was continuously loaded for rail shipment hot from Pittsburgh mills to accommodate limited materials storage areas near the city construction site, and so, that steel delivered had sufficiently cooled to immediately use.

Typical of other skyscrapers of the 1930’s it features the art-deco design of pre-World War II New York City architecture. As part of its design the 102 nd floor of the Empire State Building has a door with ascending stairs leading to the 103 rd floor originally built with a mast to moor dirigibles and airships. Due to numerous safety problems of airships the mast was never used for its purpose.

Copyright © DigitMath.com

All Rights Reserved.