The Trigonometry of a Tangent Graph

The graph of a tangent function is periodic with period π and differs from the 2π period of the sine graph and cosine graph.

Tangent graph showing its period π:

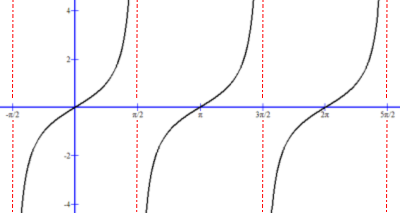
To understand why the tangent function graph has a period of π we first look at the definition of the tangent function:

tan θ = sin θ / cos θ

This definition of tangent is identical to the definition provided by SOH-CAH-TOA:

1. sin θ = opposite / hypotenuse = o / h
2. cos θ = adjacent / hypotenuse = a / h
3. tan θ = sin θ / cos θ  = (o / h) / (a / h) = opposite / adjacent

The numerator of the tangent function, the sin θ, is zero when θ = 0, ±π, ±2π … and so on. At each of these sine values the tangent equals zero and is when a tangent graph line intersects the horizontal x-axis.

The cos θ is the denominator of the tangent function. The cos θ is zero when θ = ±π/2, ±3π/2, ±5π/2, … and so on. The tangent is not defined for these values of θ since a fraction denominator of zero is undefined math and explains why the tangent graph lines approach, but never reach cos θ = 0 value.

From the tangent function definition it can also be seen that when the sin θ = cos θ, at π/4 radians (45°), the tan θ equals 1. Then, for the interval 0 ≤ θ < π/4 the tangent is less than 1 and for the interval π/4 < θ < π/2 the tangent is greater than 1.

Because the sin θ is an odd function and the cos θ is an even function the tangent is an odd function; odd divided by even is odd. Then, for all θ in the domain of the tangent:

1. tan (−θ) = sin (−θ) / cos (−θ) = −sin θ / cos θ = −tan θ
2. tan (θ + π) = sin (θ + π) / cos (θ + π) = −sin θ / −cos θ = tan θ

From these equations we see that π is the smallest positive number p for which the tan (θ + p) = tan θ, because tan 0 = tan π = 0. Therefore, the tangent function has period π, and a tangent graph repeats every π units.

Copyright © DigitMath.com

All Rights Reserved.