The Trigonometry of a Cosine Graph

The graph of a cosine function is periodic with period 2π and is similar to a graph of the sine function, with the difference that  cosine function is shifted π/2 units left of the sine function for every corresponding value.

Period function of cosine and sine (red line) showing π/2 radian units shift:

To understand this π/2 radian units shift we equate five different degree measurements of cosine to sine:

1. cos 0° = 1 = sin 90° = sin (0 + 90)°
2. cos 30° = √3 / 2 = sin 60° = sin 120° = sin (30 + 90)°
3. cos 45° = √2 / 2 = sin 45° = sin 135° = sin (45 + 90)°
4. cos 60° = ½ = sin 30° = sin 150° = sin (60 + 90)°
5. cos 90° = 0 = sin 180° = sin (90 + 90)°

Observe that in each value of corresponding cosine values equated to sine values that:

cos A° = sin (A + 90)°
or, in radian measure,
cos θ = sin (θ + π / 2)

… and it is this relationship that allows us to draw the cosine graph by shifting the sine graph by π/2 units to the left.

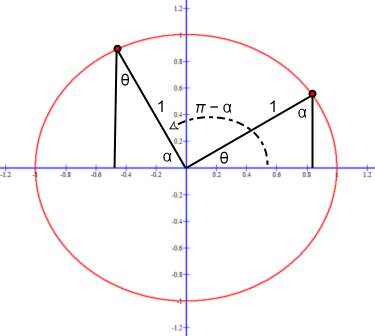
The π/2 shift of sine that equates the sine graph to the cosine graph can also be shown on a unit circle.

This unit circle shows the cos θ = sin α = sin (π − α) = sin (θ + π / 2):

Copyright © DigitMath.com

All Rights Reserved.