Parabolas and Conics

The conics general formula of a quadratic equation in two unknowns is:

Ax2 + Bxy + Cy2 + Dx + Ey + F = 0 when A, B and C are not all zeros.

The graph of the quadratic function y = ax2 + bx + c when a ≠ 0, is a parabola which opens up or down. A quadratic equation with a y2 term and no x2 term is a parabola which opens to the left or right.

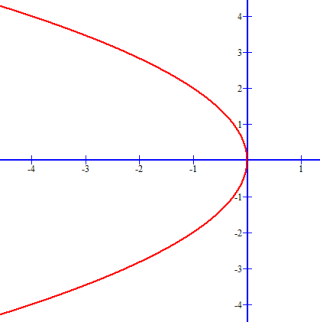
−y2 − 4x = 0 is a parabola that opens to the left:

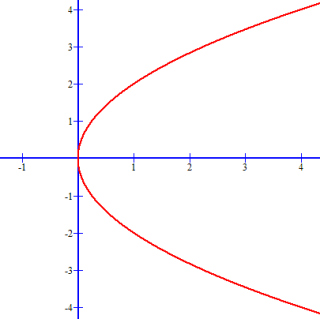
y2 − 4x = 0 is a parabola that opens to the right:

A parabola is defined as the locus of all points equidistant from a fixed point and a fixed line. The point is the focus of the parabola and the line is the directrix:

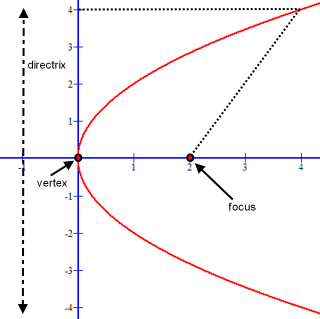
Standard Formula of the Equation of a Parabola:

By observing at the standard form of the equation we can determine the direction a parabola will open.

y2 = 4px     If p is positive, the parabola opens to the right. If p is negative the parabola opens to the left. The vertex is (0, 0) and the axis is the x-axis.

x2 = 4py     If p is positive the parabola opens up. If p is negative the parabola opens down. The vertex is (0, 0) and the axis is the y-axis.

The value of p is the distance from the vertex to the focus of the parabola. A focus always lies on the axis of its parabola.
The equation y2 = 4px above indicates that p = +1 and so the focus is 1 unit to the right of the vertex at coordinate (1, 0).

If given the equation x2 = −12y and asked to determine the vertex and focus:
   a) By the equation x2 = −12y, when y = 0 then x = 0. The vertex is at (0, 0).
   b) By the standard equation x2 = 4py; then −12y = 4py and p equals −3, giving the coordinate (0, −3).

Should the vertex of a parabola be a coordinate point other than (0, 0) then we can say the vertex is coordinate (h, k) and the standard equation can be written as:

(y − k)2 = 4p(x − h)
The axis of the parabola is parallel to the x-axis. The curve opens to the right if p is positive and to the left if p is negative.

(x − h)2 = 4p(y − k)
The axis of the parabola is parallel to the y-axis. The curve opens up if p is positive and down if p is negative.

If given the equation (y − 3)2 = −4(x − 2) and asked to determine the vertex and focus:
    (Note that p is negative as seen by the minus sign beginning the term −4(x − 2); this parabola opens left)
a) By the equation (y − 3)2 = −4(x − 2), when y = 3 then x = 2. The vertex, (h, k), is at (2, 3).
b) By the standard equation (y − k)2 = 4(x − h); then 4(x − h) = −4(0 − 2) = −4(− 2) =  8,
        then 4p = 8 and p = 2
 Since this parabola opens left, its focus is a horizontal distance left of the vertex; p = 2 so the focus coordinate is (0, 3).

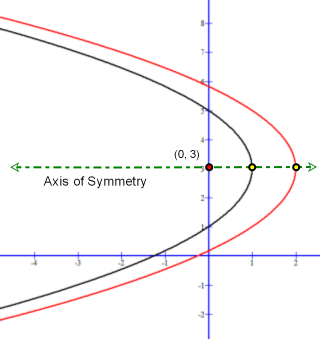
Graphs of parabolas (y − 3)2 = −4(x − 2) and (y − 3)2 = −4(x − 2) share the same
focus (red dot), but have different vertex (yellow dots):

Equating the Parabola General Formula to the Standard Formula of the Equation:

If the  equation of a parabola is in general form we must complete the square to get the equation in standard form. To accomplish this we will begin with the general form equation x2 + 2y − 4y − 3 = 0. It is the general form of a parabola since only one term, x, is squared. The conics general math equation, Ax2 + Bxy + Cy2 + Dx + Ey + F = 0, has two variables squared.

x2 + 2x − 4y − 3 = 0  →  x2 + 2x = 4y + 3  →  x2 + 2x + 1 = 4y + 3 + 1  →  (x + 1)2 = 4(y + 1)

We can now see by the standard equation that the vertex is at coordinate (−1, −1). The axis is parallel to the y-axis and the parabola opens up. Also, by the standard equation
(x − h)2 = 4p(y − k); 4(y − k) = −4(0 − 1) = −4(− 1) =  4, then 4p = 4 and p = 1.
The focus is 1 up from the vertex at (−1, 0).

There are Many Uses of Parabolas in Industry and Science. A few applications are:

1. Some of the largest steel bridges are built with parabolic arches.
2. The path traveled by a projectile, neglecting air resistance, is parabolic.
3. The relation between the distance a falling body travels and the time required is the equation of a parabola.

Copyright © DigitMath.com

All Rights Reserved.