



Matrices and Determinants



Arthur Cayley
Around 1858 a British mathematician, Arthur Cayley, invented matrices and was instrumental in the development of determinants. He was a Cambridge University graduate and a lawyer by profession. His insights into matrices came as he studied theory of transformations. Arthur Cayley and two American mathematicians, Benjamin Pierce and Charles Pierce (Benjamin’s son) are credited with developing Matrix Algebra.
Matrix Basics and Definition of a Matrix:
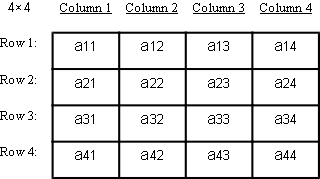
A Matrix is an array with each element organized by unique rows m and columns n, where m and n are integers. A matrix having m rows and n columns is said to have an order of m×n. Each element of an array can be addressed by its unique row and column subscript which forms a double subscript aij.
A matrix that has only one row, m = 1, is a row matrix. A matrix that has only one column, n = 1, is a column matrix.
When the number of array rows and columns are equal it is a square matrix, 1 ≤ m and m = n. An array of order 4×4 with its 4 rows and 4 columns is a square matrix.
The purpose of an array is to organize data by some meaningful order. For mathematics the data is numerical and operations can be performed on the numerical data.
A matrix derived from a system of linear equations is the augmented matrix of the system. The matrix derived from the coefficients of the augmented matrix is the coefficient matrix of the system:
Augmented Matrix
3×4 | x | y | z | = c |
Row 1: | 1 | −4 | 3 | 5 |
Row 2: | −1 | 3 | −1 | −3 |
Row 3: | 2 | 0 | −4 | 6 |
System of Linear Equations
x − 4y + 3z = 5
−x − z + 3y = −3
2x − 4z = 6
The augmented matrix has order 3×4. Note that 0 has been placed in row 3 of the matrix for the missing y term of the 2x − 4z = 6 equation.
Coefficient Matrix
3×3 | x | y | z |
Row 1: | 1 | −4 | 3 |
Row 2: | −1 | 3 | −1 |
Row 3: | 2 | 0 | −4 |
The coefficient matrix has order 3×3. Note that constant terms of the linear equations are never included in a coefficient matrix.
Array Row Echelon Form and Reduced Row Echelon Form:
The term echelon refers to a stair-step pattern formed by non-zero elements of a matrix.
A Matrix in row-echelon form has five properties:
- Rows that are entirely zeros are the bottom rows of the matrix.
- Each row that is not entirely zeros the first non-zero entry is 1.
- A row with a leading 1; all rows beneath that same column is zeros.
- A row with a leading zero; all rows beneath that same column is zeros.
- For two consecutive rows the leading 1 of the higher row is left the leading 1 of the lower row.
Two matrices that are in row-echelon form:
Matrix 1 Row Echelon Form
3×4 | Column 1 | Column 2 | Column 3 | Column 4 |
Row 1: | 1 | 3 | −2 | 4 |
Row 2: | 0 | 1 | 0 | 2 |
Row 3: | 0 | 0 | 1 | 5 |
Matrix 2 Row Echelon Form
4×5 | Column 1 | Column 2 | Column 3 | Column 4 | Column 5 |
Row 1: | 1 | −3 | 7 | 6 | −2 |
Row 2: | 0 | 0 | 1 | 4 | 2 |
Row 3: | 0 | 0 | 0 | 1 | 3 |
Row 4: | 0 | 0 | 0 | 0 | 1 |
A matrix in row-echelon form is in reduced row-echelon form if every column that has a leading 1 has zeros in every position above and below the leading 1.
Two matrices that are in reduced row-echelon form:
Matrix 1 Reduced Row Echelon Form
3×4 | Column 1 | Column 2 | Column 3 | Column 4 |
Row 1: | 0 | 1 | 0 | 4 |
Row 2: | 0 | 0 | 1 | 2 |
Row 3: | 0 | 0 | 0 | 0 |
Matrix 2 Reduced Row Echelon Form
4×4 | Column 1 | Column 2 | Column 3 | Column 4 |
Row 1: | 1 | 0 | 0 | −1 |
Row 2: | 0 | 1 | 0 | 3 |
Row 3: | 0 | 0 | 1 | −2 |
Row 4: | 0 | 0 | 0 | 0 |
Definition of a Determinant:
The use of determinants develops from number patterns that emerge when systems of linear equations are solved. Every square matrix can be associated with a real number determinant. The use of a determinant to solve a system of equations is algorithmic rather than mathematical and determinants are important to solve linear equation systems by Cramer’s Rule.
Copyright © DigitMath.com
All Rights Reserved.
| 3×3 Matrix Determinant |
| 4×4 Matrix Determinant |
| 3×3 Cramer’s Rule |