Conics Circle

A conic section circle is formed when a plane slices a cone perpendicular to the axis of a cone. It can be viewed as a “special case” Ellipse. This makes the circle a good starting point for Conics study.

Standard Form of the Equation of a Circle:

We define a circle as the locus of all points equidistant from a fixed point.

Let P0 :(h, k) be any fixed point of a plane and r any positive real number. Now consider that the center of the circle is P0 :(h, k) and radius r is simply the set S of all points P :(x, y) in the plane so that the distance between P0 :(h, k) and P :(x, y) is any point on S. Then, recalling the distance formula:

√ [ (x − h)2 + (y − k)2 ] = r

Then,

(x − h)2 + (y − k)2 = r2 provided r ≥ 0

Thus, a point P0 :(x, y) lies on circle S if,

(x − h)2 + (y − k)2 = r2

It is the standard formula equation of a circle.

Visual showing locus point P0, radius r, and any point P on the circumference for circle equation x2 + y2 = 25:

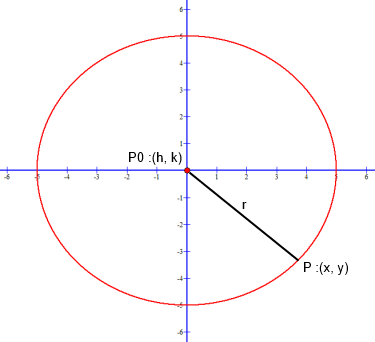
Understanding and using the Standard Form Equation of a Circle

By the standard form equation (x − h)2 + (y − k)2 = r2:
h = 0, k = 0, r2 = 25 and the radius r = √25 = 5

Visual showing locus point P0, radius r, and any point P on the circumference for circle equation (x − 2 )2 + (y + 3)2 = 16:

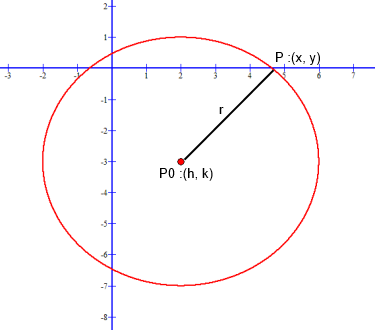
Conic Circle with locus coordinate (2 , -3) and radius of 4

By the standard form equation (x − h)2 + (y − k)2 = r2; h = −2, k = 3 and the radius, r = √16 = 4.

Can you see by the (x − h)2 term that x = 2 and by the (y − k)2 term that y = −3? By making x − h = 0 and y − k = 0 provides the Cartesian coordinate point relative to (0, 0), the locus of the circle.

Equating the Standard Form of the Equation of a Circle to the Conics General Math Definition:

If we were asked to write the equation of a circle with its center at (3, −1) and radius 2:

We would use the Standard Form Equation and write
(x − 3)2 + (y − (−1))2 = 22 or (x − 3)2 + (y + 1)2 = 22

By factoring
(x − 3)2 + (y + 1)2 = 22 = (x − 3) (x − 3) + (y + 1) (y + 1) = 4
and then combining like terms, the result is:
x2 + y2 − 6x + 2y + 6 = 0
and is the general form equation for a circle.

Finally, by comparing the conics general math definition to the general form equation for a circle:
(recall from the conic sections page we are only dealing with equations where B = 0)
Ax2 + Bxy + Cy2 + Dx + Ey + F = 0
x2 + y2 - 6x + 2y + 6 = 0
then,
Ax2 + Cy2 + Dx + Ey + F = 0
represents a circle when A = C and A ≠ 0.

Top of Page

About Privacy