



Absolute Value


Absolute Value is defined as:
|x| = x when x ≥ 0
|x| = −x when x < 0
|0| = 0 (zero is not positive or negative)
According to this definition the |x| is always greater than or equal to zero for all real numbers.
If you were asked to determine the absolute value of 5 and −5 (or any real number):
|5| = 5
|−5| = − (−5) = 5
We can also solve equations that involve absolute value:
|x + 2| = 4
To solve this equation we must evaluate
|x + 2| ≥ 0 and |x + 2| < 0. This is because, by definition, the absolute value of x + 2 can be either x + 2 or − (x + 2).
Case 1: When x + 2 = 4 then x = 2 and is a solution of the equation since 2 ≥ 0.
Case 2: When − (x + 2) = 4 then −x − 2 = 4.
−x = 4 + 2
x = − (4 + 2)
x = −6
The equation solution set for |x + 2| = 4 is {2, −6}.
To solve for x in the equation |2x − 1| = 3x + 4:
Case 1: When 2x − 1 ≥ 0 we simply solve for x in the equation 2x − 1 = 3x + 4.
−1 − 4 = 3x − 2x
−5 = x
Case 2: When 2x − 1 < 0 then − (2x − 1) = 3x + 4.
−2x + 1 = 3x + 4
1 − 4 = 3x + 2x
−3 = 5x
−3/5 = x
Absolute Value Function
When discussing Absolute Value as a math function we consider equations involving inequality symbols and therefore should first understand how to solve linear inequality equations.
To begin let’s examine the graph of f(x) = |x| so that y = f(x) = |x|:
We observe that this graph consists of two rays which begin at the origin and that each line ray (red) bisect one of the right angles formed by the Cartesian coordinate axes (blue). The line in the first quadrant is the graph of f(x) = |x| when x ≥ 0 and the line in the second quadrant is f(x) = |x| when x < 0. The Absolute Value Function is not a one-to-one function since f(x) = |x| = x and f(−x) = |−x| = x so that f(x) = f(−x) even though x ≠ −x. Thus, the graph of f(x) = |x| shows us the domain of x is all real numbers (positive, negative or 0), while the range y is all real numbers greater than or equal to zero.
Graph of Absolute Value Function f(x) = |x|:
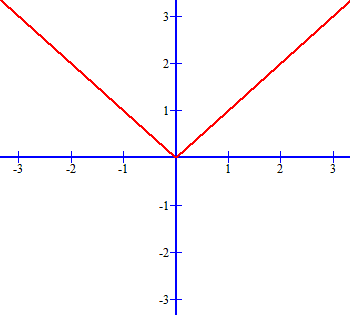
A Graph of Absolute Value is always shaped “V” like.
From the observations of graph f(x) = |x| we can state:
|x| ≥ x and |x| ≥ −x
Or can be stated as,
x ≤ |x| and −x ≤ x
The result of combining both inequalities (for all real numbers x):
−x ≤ x ≤ |x|
The Absolute Value of a Sum is Always Less Than or Equal To the Sum of The Absolute Values
Consider |x1 + x2| where x1 and x2 are real numbers; positive, negative or zero:
−|x1| + (−|x2|) ≤ x1 + x2 ≤ |x1| + |x2|
Becomes,
− (|x1| + |x2|) ≤ x1 + x2 ≤ |x1| + |x2|
By multiplying −1 by the first inequality:
− [− (|x1| + |x2|) ≤ x1 + x2] = |x1| + |x2| ≥ − (x1 + x2)
The result of multiplying the inequality equation by −1 reversed the direction of the inequality from ≤ to ≥. Rewrite the inequality as less than or equal to:
− (x1 + x2) ≤ |x1| + |x2|
Now, consider the second inequality of equation −|x1| + (−|x2|) ≤ x1 + x2 ≤ |x1| + |x2|:
x1 + x2 ≤ |x1| + |x2|
And, consider the definition of absolute value; that |(x1 + x2)| is always equal to (x1 + x2) or − (x1 + x2).
This provides:
|x1 + x2| ≤ |x1| + |x2|
This result shows us the absolute value of a sum is always less than or equal to the sum of the absolute values.
As an example:
|4 + 6| = |4| + |6|
10 =10
While,
|4 + (−6)| < |4| + |−6|
2 < 10
By also considering the rules for math subtraction the absolute value equation, |x1 + x2| ≤ |x1| + |x2| for all real number x1 and x2, can be extended and written as:
|x1 ± x2| ≤ |x1| + |x2| for all real number x1 and x2.
This tells us the absolute value of a sum or difference is at most the sum of its absolute values.
The Absolute Value of a Product
From the definition of Absolute Value, that |x| ≥ 0 the product is always:
|x1 x2| = |x1| |x2| for all real numbers positive, negative or zero.
|x1 / x2| = |x1| / |x2| if x2 ≠ 0
Copyright © DigitMath.com
All Rights Reserved.