



Pascal’s Triangle for Binomial Expansion


When we write the coefficients for a binomial that is raised to a power, (a + b)n , we expand that binomial. Pascal’s Triangle is a convenient way to remember the pattern for expanding binomial coefficients. These are the same coefficients that had been determined by Factorial math until the French mathematician Blaise Pascal in the mid-sixteen hundreds introduced the coefficient triangle to the Western world. Prior to this introduction the Chinese text Precious Mirror diagrams Binomial Expansions.
Pascal’s Triangle:
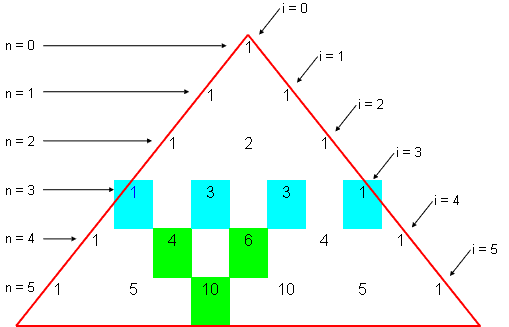
The elegance of Pascal’s Triangle is the simplicity it provides to expedite a Binomial Expansion regardless of the number of terms. If we were to consider (a + b)3 using factorials the binomial expansion would look as:
(a + b)3 =
(
3
0
)
a3b0 +
(
3
1
)
a2b1 +
(
3
2
)
a1b2 +
(
3
3
)
a0b3
We would next determine the values of each factorial quotient:
(
3
0
)
=
(
3
1
)
=
(
3
2
)
=
(
3
3
)
=
Giving us the binomial coefficients for each term of the binomial expansion.
By using Pascal’s Triangle there is no need to evaluate factorial quotients. The triangle provides us the binomial coefficients, the powers of a and b of each term, and the number of terms for the resulting (a + b)n expansion formula. All we need to do is to first look at the row of the triangle corresponding to the value of n. This provides us the binomial coefficients. For n = 3 the coefficients are: 1,3,3,1. This also tells us the resulting binomial formula will have 4 terms:
(a + b)3 = 1a3 + 3a2b + 3ab2 + 1b3
For (a + b)3 the binomial expansion powers of a are provided by n = 3 and proceed for each subsequent term as decreasing by 1. The powers of b are given by i of Pascal’s Triangle and increase by 1 for each subsequent term. The same methodology works regardless of the value of n of (a + b)n.
If we need to create Pascal’s Triangle the left and right side of the triangle for any row is always 1 and the top of the triangle is always 1. Each coefficient of a row is determined by adding the coefficients left and right of the row above. As an example, reference the 10 highlighted in the row for n = 5. By adding the 4 and 6 of the row above provides the coefficient 10. All coefficients are tabulated in this manner. This tabulation manner also explains why the right and left sides of the triangle are always 1, for the left side there is no coefficient to the left on the row above and for the right side there is no coefficient to the right on the row above.
The Triangle above shows the coefficients for (a + b)0 through (a + b)5. We can now easily calculate the coefficients for (a + b)6, the coefficients are: 1, 6, 15, 20, 15, 6, 1. Pascal’s Triangle can accommodate all Binomial Expansions (a + b)n.
Copyright © DigitMath.com
All Rights Reserved.