Graphing Linear Equations

Graphing Linear Equations is a mapping process to diagram straight lines as objects. Mathematicians often diagram using Cartesian Coordinate Systems.

A Cartesian Coordinate System provides a central point of reference for an object and between objects. Cartesian Coordinate Systems are drawn by a horizontal x line bisecting a y line forming a 90 degree right angle. Coordinates x and y are on a single plane, a flat surface.

The slope of a straight line is a measure of steepness. Slope is described by a change in Rise, divided by a change in Run.

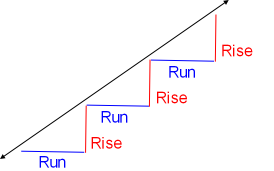
Slope = Rise / Run

“To graph or solve Linear Equations use the Slope-Intercept Form:

y = mx + b

Where m is the line slope, x is a coordinate value along the x axis and b is the y intercept.”

Many run and rise together look like stairs.

Rise is a distance Δy as y2 − y1, and Run is a distance Δx as x2 − x1 (Reference diagram at right).

Suppose coordinates (8, 7) and (4, 4), the slope, Δy / Δx, is:

(y2 − y1) / (x2 − x1) =

(7 − 4) / (8 − 4) =

3/4

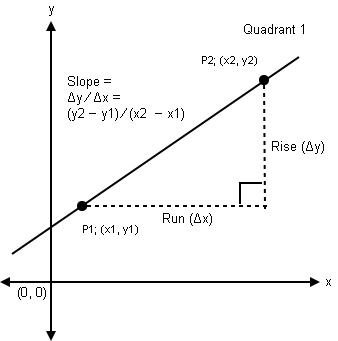
Graph of line showing linear slope as Δy / Δx.

How to Graph Linear Equations

By plugging values of x into a Linear Equation gives values of y.

Several coordinate solutions for y = 3x + 2:

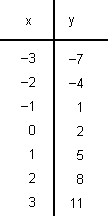
“Y” values for “x” integer values −3 thru 3.

Choose two x and y coordinate solutions. Use them as points through which to plot the line.

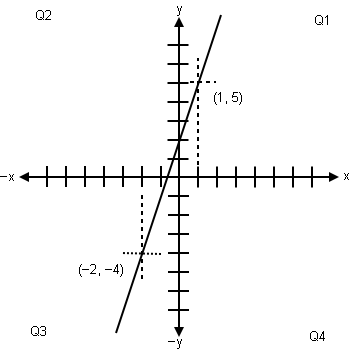
Graph of straight line equation y = 3x + 2 using coordinates (1, 5) and (−2, −4).

From the image directly above we already know that (1, 5) and (−2, −4) are two coordinate points of Linear Equation y = 3x + 2. But, what if we only knew the two coordinate points, not the equation? Yes, we can create the equation by applying the Slope-Intercept Form y = mx + b:

First determine the line slope…

m = (y2 − y1) / (x2 − x1) = (5 − (−4)) / (1 − (−2)) = 9 / 3 = 3

and plug the slope, m , into the Slope-Intercept Equation y = mx + b.

y = 3x + b

Next determine b, the y intercept. To do this use any coordinate along the line and plug the x and y values into the Slope-Intercept Equation (I’m going to use coordinate (1, 5) ) …

5 = 3 (1) + b

5 − 3 = b

2 = b

And we can now write y = 3x + 2, the Linear Equation defined by line segment coordinate points (1, 5) and (−2, −4).

Copyright © DigitMath.com

All Rights Reserved.