Hyperbolas and Conics

The hyperbola conic section is formed when a plane intersects a double-napped cone parallel to the axis of the cones. A geometric diagram of the hyperbola can be viewed on the Conic Sections page.

If the conics general quadratic equation Ax2 + Cy2 + Dx + Ey + F = 0 has two variables squared and the coefficients (A and C) of the squared variables have opposite signs, the graph of the equation is a hyperbola.

The equations x2 − y2 = 4 and x2 − 3y2 + 6x + 6y − 8 = 0 are both hyperbola equations. The first equation has coefficients D and E that are zero.

Standard Formula Equation of the Hyperbola:

The hyperbola has two branches that open away from a center point. The standard form of the equation of a hyperbola that has its center at origin, (0, 0), and opens left and right is:

x2 / a2 − y2 / b2 = 1

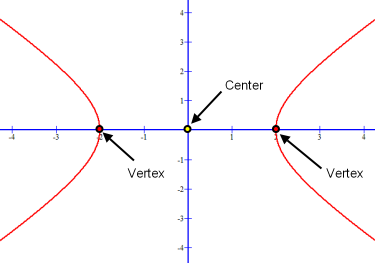
As can be seen in the image to the right of x2 / a2 − y2 / b2 = 1; this equation intersects the x-axis at distance “a” left and right the center of the hyperbola. Each intersection is a vertex of the hyperbola with the center at the Cartesian coordinate origin. The axis joining these vertices, the x-axis, of the hyperbola is the transverse axis. This hyperbola is also symmetric about its conjugate y-axis, but does not intersect this axis.

Vertices: (−a, 0) and (a, 0)

Foci: (−√ (a2 − b2), 0) and (√ (a2 − b2), 0)

Center: (0, 0)

Transverse Axis: x axis (or, y = 0)

Conjugate Axis: y axis (or, x = 0)

Graph of hyperbola equation x2 / a2 − y2 / b2 = 1
when a = 2 and b = 2:

The size of the transverse axis is not necessarily larger than the conjugate axis. It may be longer, shorter or the same length as the conjugate axis, however, the direction the hyperbola opens is affected by which term, the x2 or y2 term, is positive when the equation is in standard form:

An equation of the standard form …

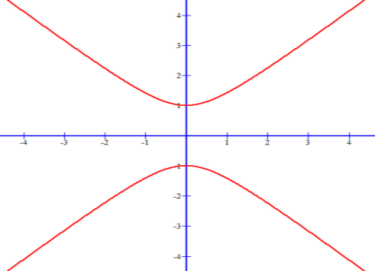
x2 / ( )2 − y2 / ( )2 = 1

…is a hyperbola that always opens to the left and right.

An equation of the standard form …

y2 / ( )2 − x2 / ( )2 = 1

…is a hyperbola that always opens up and down.

Graph of hyperbola equation x2 / 12 − y2 / 12 = 1
opens left and right:

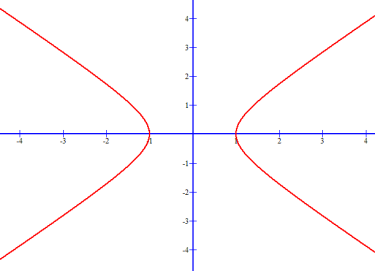
Graph of hyperbola equation y2 / 12 − x2 / 12 = 1
opens up and down:

Hyperbola Equation Form xy = c:

The general quadratic equation, Ax2 + Bxy + Cy2 + Dx + Ey + F = 0, is provided on the Conic Sections page. It is on this page stated that we would only work with equations where B = 0. The xy term of the conics general math equation would therefore equal zero.

However, the hyperbolic form xy = c is important to recognize…

If c ˃ 0, the graph of the hyperbola will have its vertices in quadrants 2 and 4 with its center the Cartesian coordinate origin. If c < 0, the graph of the hyperbola will have its vertices in quadrants 1 and 3 with a center the Cartesian coordinate origin.

Hyperbolas Have Many Uses:

There are many uses of hyperbolas covering a wide spectrum of applications; a few are listed here…

1. Alpha particles shot near an atomic nucleus follow a hyperbolic path.
2. Electrostatic force repulsion and magnetic repulsion forces are hyperbolic.
3. The equation PV = C, expressing Boyle’s Law, has a hyperbolic graph whose asymptotes are coordinate axes.
4. The hyperbola is used to locate source of sound, or for radio location and guidance of planes and ships based
   on the time delay of radio signals received from two points.
5. A type of reflecting telescope has a hyperbolic mirror to reflect the image to its eyepiece.

Copyright © DigitMath.com

All Rights Reserved.