Digit Math Mobile Website top of page banner image

Mobile Math Website

Two Variable Linear Equations

Linear Equations having two variables, where both variables are unknown quantity, provide Cartesian coordinates, (x, y), to graph a straight line.

The independent variable is x and dependent variable is y. A value of y depends on a value assigned x to solve the equation.

To solve Linear Equations in two variables isolate the dependent variable to one side of the equation as a lone term. The value of the isolated variable is determined when value is assigned to the independent variable as the following problems demonstrate:

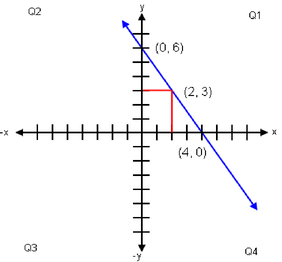
Two variable linear equation with negative slope when graphed.

Graph of linear equation 3x + 2y = 12

3x + 2y = 12

2y = 12 − 3x

y = (12 − 3x ) / 2

y = 6 − 3/2 x

x = 0, y = 6 (y intercept when x is zero)
x = 2, y = 3

x = 4, y = 0 (x intercept when y is zero)
Slope: −3/2.

A straight line having a negative slope and passing through Cartesian Coordinate System quadrants 2, 1 and 4.

The y intercept is above (0, 0), and x intercept is right of (0, 0). The slope of the line is negative, slants from higher left to lower right.

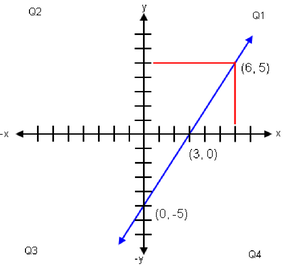
Graph of linear equation 5x − 3y = 15

5x − 3y = 15

5x − 15 = 3y

(5x − 15) / 3 = y

5/3 x − 5 = y

x = 0, y = −5 (y intercept)

x = 3, y = 0 (x intercept)

x = 6, y = 5

Slope: 5/3.

A straight line having a positive slope and passing through Cartesian coordinate system quadrants 3, 4 and 1.

Why? The y intercept is below (0, 0), and x intercept is right of (0, 0). The slope of the line is positive, slants from lower left to higher right.

Top of Page About Us Privacy