 Sitemap
SitemapMobile Math Website
Math Radicals
Radicals are an irrational form that equate to a rational or irrational number or expression. They can be expressed as fractional exponents that provides the convenience of not requiring a radical symbol. Most math of radicals is to change them to their simplest form to reduce complexity.
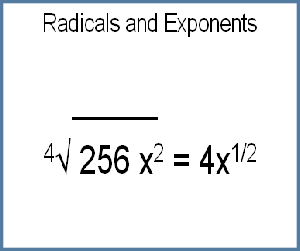
Radical Definition
n√ a is the general notation for the nth root of “a”. If n = 2 the index is not usually written, a square root is assumed. “a” is the radicand. The √ symbol denotes a radical.
The principal nth root of a positive number is the positive root. The square root of 9 has 2 root numbers 3 and −3, only 3 is a principal root.
The principal nth root of zero is zero. Just says any root of zero is zero.
The principal nth root of a negative number is the negative root when n is odd. The cube root of −27 is −3, because the index 3 is odd:
3√ −27 = −3, because the index is an odd number: (−3) (−3) (−3) = −27
√ −25 = nonsense. A square root is an even number index. Whether (5) (5) is multiplied or (−5) (−5), the result is positive 25.
−√ 25 = −5. The square root of 25 is 5 or −5, the minus sign outside the radical indicates the negative of the root.
2√ 16 = 4
3√ −8 = −2
n√ 0 = 0
Equating Exponents and Radicals / Fractional Exponents
Radicals can be expressed as fractional exponents, and fractional exponents can be transformed to irrational radical form. The index of the radical, “n”, becomes the denominator of the fractional exponent:
n√ a = a1/n
n√ am = am/n
Examples:
√ x2 = x2/2 = x1 = x
(125m)2/3 = 25 3√ m2
3√ (ab)2 = (ab)2/3
3√ 729 = (3)2 = 9
3√ 729 = 272/3 = 9
3√ y27 = y27/3 = y9
Let y = 3, the cube root of 327 = 19,683 = 39
3√ x6 = x6/3 = x2
Let x =2, the cube root of 26 = 4 = 22
3√ (−27 x6 y3) = −271/3 x6/3 y3/3 = −3 x2 y, because (−3 x2 y)3 = −27 x6 y3
Copyright © DigitMath.com
All Rights Reserved.