 Sitemap
SitemapMobile Math Website
Radian Measure
including How to Convert Radians to Degrees and the Trigonometric Functions of Special Angles
It is preferable to have trigonometric functions (sine, cosine, tangent, etc.) defined so the domain of each function is the set of all possible real numbers. Generally, when we speak of degrees and minutes it is an acute angle, an angle that is less than 90°. This limits us to the increments of degrees and minutes. Radian Measure is not based upon increment and thus radian measure includes all possible real numbers.
Radian measure is direct result of a central angle that has its vertex at the center of a unit circle, a circle having a radius of one:
Unit circle (equation x2 + y2 = 1):
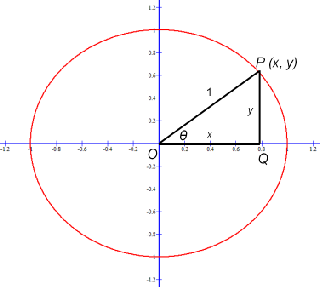
If we consider point P on a unit circle in the first quadrant:
cos

QOP = adjacent / hypotenuse
cos

QOP = x / 1 = x
sin

QOP = opposite / hypotenuse
sin

QOP = y / 1 = y
Let θ (theta) =

QOP, then
P = (x, y) = (cos θ, sin θ)
The coordinates of P are the cosine and sine of angle θ.
Angle θ is the central angle, an angle formed by two radii of a circle. The measure of a central angle is proportional to the length of a circle between the two points of each radius.
From this a radian is defined as the measure of the central angle that subtends an arc whose length is that of the radius. For a unit circle that length is one unit.
The length of the subtended arc equals the length of the radius on a unit circle.
θ = 1 radian = 57.296°:
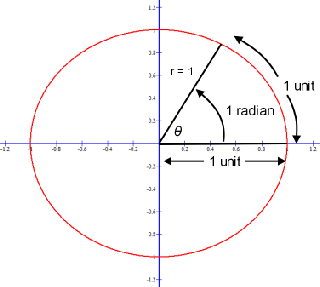
With radian measure we are working with radius not diameter. The circumference of a circle is often stated as the ratio of circumference, C, to its diameter, d; C = πd. With radian measure C = 2π r, where r is a radius and 2r = d.
Equating Radians to Degrees
or Degrees to Radians:
Because the unit circle radius is one its circumference, C = 2π r is 2π. Then, by proportionality, 2π radians is 360°, π radians is 180°.
We can state this proportionality between degrees and radians as:
1 radian = π / π radian = 180° / π.
1 radian = 180° / 3.1415826 = 57.296° or 57.3°
To convert from degrees to radians:
Multiply degrees by π / 180°
To convert from radians to degrees:
Multiply radians by 180° / π.
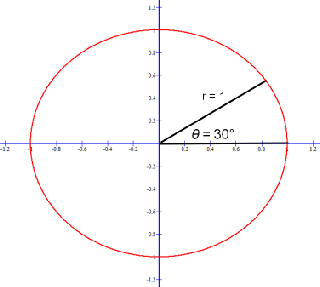
An angle is in standard position when the vertex is at origin, the center of the circle and one side, the initial side, is positive x-axis. The angle is positive if the other side, the terminal side, is measured in a counterclockwise direction. The angle is negative if measured in a clockwise direction:
Positive angle 30° is π / 6 radians:
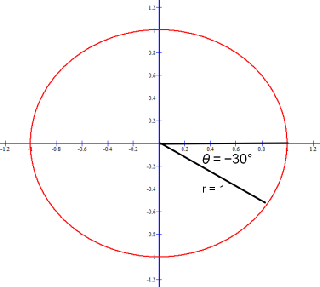
Negative angle 30° is −π / 6 radians:
Radians and the Trigonometric Functions:
In physical science applications there is often a need to work with time and the ability to state the cosine t and the sine t, where t is a number of seconds. For this and other purpose the trigonometric functions can be extended so as to apply to any number of radians. This was shown for a point, P; P = (x, y) = (cos θ, sin θ). The coordinates of P are the cosine and sine of central angle θ. The terminal side of the angle intersects the unit circle at P, with coordinates (x, y). The cosine θ is defined to be x and the sine θ is defined to be y. This means that the cos and sin of any possible number is defined.
By proportionality we already know that:
4π / 2 = 2π radians is 360°,
3π / 2 radians is 270°,
π radians is 180°, and
π / 2 radians is 90°.
For these angles their point, P, values for x and y can only be 1, −1 or 0. These angles define a terminal side that is on the x or y axis, respectively the cos θ or sin θ.
cos θ and sin θ for 90°, 180°, 270° and 360°:
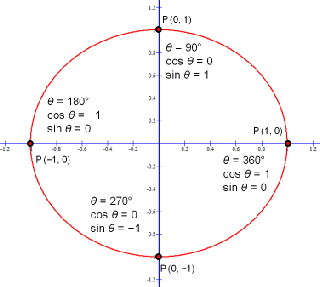
All other angles are acute having the initial side along the x-axis from the circle coordinate center (standard position) and a terminal side not parallel the x-axis or y-axis. By this definition we only need consider the coordinate quadrant (I, II, III or IV) to determine the positive or negative sign of the cos θ and sin θ.
Trigonometric Functions of
Special Angles:
quadrant | radians | degrees | sine | cosine | tangent |
0 | 0° | 0 | 1 | 0 | |
I | π / 6 | 30° | 1 / 2 | √3 / 2 | 1 |
I | π / 4 | 45° | √2 / 2 | √2 / 2 | 1 |
I | π / 3 | 60° | √3 / 2 | 1 / 2 | √3 |
π / 2 | 90° | 1 | 0 | undefined | |
II | 2π / 3 | 120° | √3 / 2 | −1 / 2 | −√3 |
II | 3π / 4 | 135° | √2 / 2 | −√2 / 2 | −1 |
II | 5π / 6 | 150° | 1 / 2 | −√3 / 2 | −√3 / 3 |
π | 180° | 0 | −1 | 0 | |
III | 7π / 6 | 210° | −1 / 2 | −√3 / 2 | √3 / 3 |
III | 5π / 4 | 225° | −√2 / 2 | −√2 / 2 | 1 |
III | 4π / 3 | 240° | −√3 / 2 | −1 / 2 | √3 |
3π / 2 | 270° | −1 | 0 | undefined | |
IV | 5π / 3 | 300° | −√3 / 2 | 1 / 2 | −√3 |
IV | 7π / 4 | 315° | −√2 / 2 | √2 / 2 | −1 |
IV | 11π / 6 | 330° | −1 / 2 | √3 / 2 | −√3 / 3 |
2π | 360° | 0 | 1 | 0 |
Copyright © DigitMath.com
All Rights Reserved.