Two Variable Linear Equations

Linear Equations having two variables, where both variables are unknown quantity, provide Cartesian coordinates, (x, y), to graph a straight line.

The independent variable is x and dependent variable is y. A value of y depends on a value assigned x to solve the equation.

To solve Linear Equations in two variables isolate the dependent variable to one side of the equation as a lone term. The value of the isolated variable is determined when value is assigned to the independent variable as the following problems demonstrate:

3x + 2y = 12

2y = 12 − 3x

y = (12 − 3x ) / 2

y = 6 − 3/2 x

x = 0, y = 6 (y intercept when x is zero)

x = 2, y = 3

x = 4, y = 0 (x intercept when y is zero)

Slope: −3/2.

A straight line having a negative slope and passing through Cartesian Coordinate System quadrants 2, 1 and 4.

The y intercept is above (0, 0), and x intercept is right of (0, 0). The slope of the line is negative, slants from higher left to lower right.

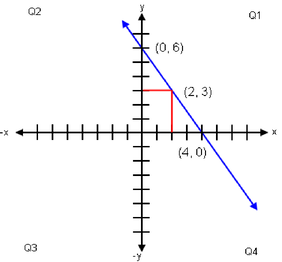
Graph of linear equation 3x + 2y = 12

5x − 3y = 15

5x − 15 = 3y

(5x − 15) / 3 = y

5/3 x − 5 = y

x = 0, y = −5 (y intercept)

x = 3, y = 0 (x intercept)

x = 6, y = 5

Slope: 5/3.

A straight line having a positive slope and passing through Cartesian coordinate system quadrants 3, 4 and 1.

Why? The “y” intercept is below (0, 0), and x intercept is right of (0, 0). The slope of the line is positive, slants from lower left to higher right.

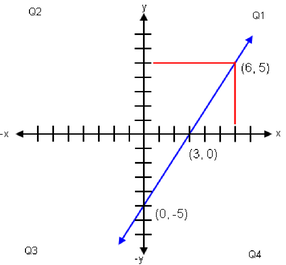
Graph of linear equation 5x − 3y = 15

Top of Page

About Privacy