 Sitemap
SitemapMobile Math Website
Parallelograms and
Quadrilaterals
A Parallelogram is defined as a four-sided plane object having opposite sides that are parallel and equal. As plane geometry figures they are flat objects on a level surface with length or height and width or base dimensions. All Parallelograms are classified as Quadrilateral.
Excellent types of Parallelogram shapes are Rectangle, Square and Rhombus.
The formula for the area of any Parallelogram is:
Area = Width × Length or Base × Height
Area of Rectangle
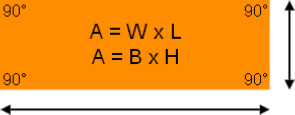
Width or Base
The Rectangle is the ideal definition of a Parallelogram with its parallel opposite sides of equal length. Opposite sides are congruent and all corners form congruent 90 degree angles.
Area of Square
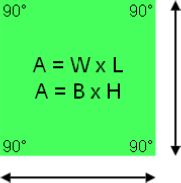
Width or Base
Square objects differ from all other Parallelograms by having all sides of equal length and each corner a 90 degree angle. All sides and all corners are congruent.
Area of Rhombus
Width or Base
The Rhombus is a special type of Parallelogram where opposite sides are parallel, all four sides are equal length and opposite angles are equal. Opposite sides and opposite corners are congruent.
The sum of angles of a Parallelogram equals 360 degrees. For the Rectangle or Square the sum total of four corners, each a 90 degree angle, give us 360 degrees.
A rhombus is different, opposite corners are equal. As a result, two opposite corners of a Rhombus will each have angles less than 90 degrees and two opposite corners will each have angles greater than 90 degrees. The more a Rhombus is leaned the larger two opposite angles become while the other two opposite angles become a like amount smaller. The sum of two opposing angles is always less than 180 degrees and greater than 0 degrees.
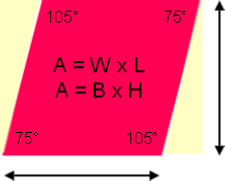
By knowing the corner to corner measurement of any side, as a straight line, and the degrees of angle at any corner we can attain the total area of a Rhombus. To explain how, suppose the red Rhombus has two opposing angles each 75°, the other opposing angles each are 105°. Also suppose the measurement of any line side from corner to corner is 5. The area can be determined by Trigonometric Sine:
Sine 75° = .965926
Sine 105° = .965926
Rhombus Area = 5 × 5 × .965926 = 24.14815
The same Trigonometric method can be applied to obtain total area of a Square object, but is unnecessary. Each corner of a Square is 90° and the Sine 90° is 1. To find the area of a Rectangle this method cannot be used. By definition a Rectangle’s Length or Height measurement differs from its Width or Base.
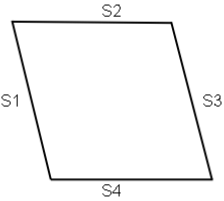
Perimeter is a total border measurement of a plane geometric figure. To find the perimeter of a Parallelogram all boundary sides are summed. If we suppose the measurement of each side of Rhombus or Square is 5 the Perimeter for the Rhombus or Square figure is 20:
Perimeter is a border measurement.
Area measures extent inside a shape’s borders:

Perimeter = S1 + S2 + S3 + S4


A Quadrilateral is a plane figure with four sides and four angles that when summed equal 360°. The less popular synonyms Tetragon and Quadrangle are sometimes used to describe a Quadrilateral shaped figure.
While all Parallelograms are Quadrilateral, not all Quadrilaterals are a Parallelogram. Types of Quadrilateral Shape that are not a Parallelogram is Trapezoid and Trapezium.
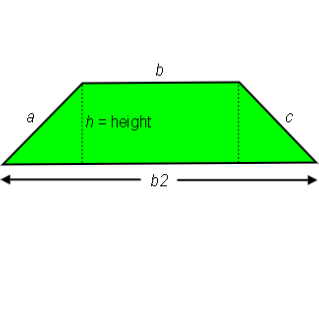
Isosceles Trapezoid:
The diagonals (line sides a and c), of an Isosceles Trapezoid are always congruent. This creates two triangles that are, except for orientation, identical. It also means the Trapezoid sides labeled b and b2 are parallel.
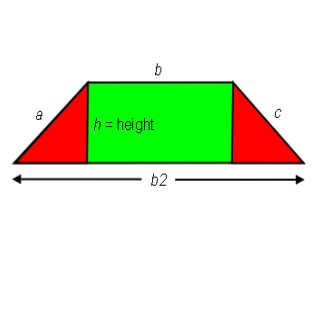
Isosceles Trapezoid highlighting left and right triangles in red:
To discover the Area of the Isosceles Trapezoid we must first understand how to measure for its width or base. By placing both triangles onto one side creates a Rectangle. The width of the Rectangle always equals ½ the sum of line sides b and b2, giving us width or base of an Isosceles Trapezoid.

Width or Base of Isosceles Trapezoid =
½ (b + b2)
Area = Width × Length or
Base × Height =
½ (b + b2) h
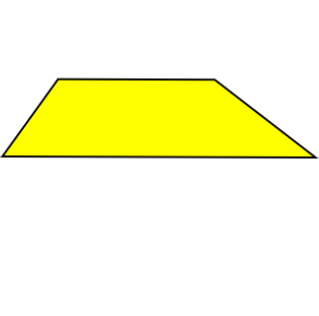
Trapezoid:
An ordinary Trapezoid does not have the symmetry of the Isosceles Trapezoid.
Trapezium:
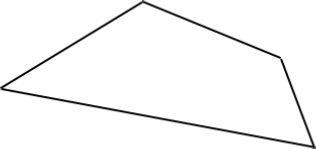
A Trapezium is a Quadrilateral without parallel sides.
Copyright © DigitMath.com
All Rights Reserved.