Mobile Math Website

Square Roots, Square
Area, Perimeters
And Triangle

A number multiplied by the same number is a square root number. If we multiply four times itself: 4 × 4 = 16. Four is the square root of 16. 16 is the squared number of 4.

The √ math symbol, a radical sign, designates square root numbers.

Square root and squared number examples:

√25  = ±5

5 × 5 = 25

(−5) × (−5) = 25

√100  = ±10

10 × 10 = 100

(−10) × (−10) = 100

√9  = ±3

3 × 3 = 9

(−3) × (−3) = 9

1. Square root numbers can be positive or negative.
2. A positive root is the principal square root.
3. An integer squared has an integer result and is a perfect square.
4. The √0 is 0.

Instead of writing radicals mathematicians often use exponents.

An exponent is a superscript number written to the right of a base number.

Squared exponent notation:

102 = 10 × 10 = 100

√100  = 1001/2 = 10

Exponents can be an integer number or fraction:

33 = 3 × 3 × 3 = 27

 3√ 27 = 271/3 = 3

The index of a radical is a superscript at the top left of the radical sign designating the root. An index of 2, a square root, is assumed if no superscript number is written.

Simplifying Square Roots

There isn’t a formula for simplifying square roots, it is a math method.

The method works if the number to simplify is not a prime number:

√12  = √(4 × 3) = √4  × √3  = 2 √3

2 √3 = 2 × 1.7320508 = 3.4641016

√12  = 3.4641016

The square root of 3 is a decimal number, not a perfect square. The easiest method to determine its square root is to use a decimal equivalent conversion table or a calculator with a square root function. The square root of 3 is: 1.7320508

To simplify non-prime integer values larger than 100 the following method is used to reduce the larger value into smaller number multiples:

√240 = √(2 × 120) = √(2 × 2 × 60) =
 √4 × √60 = 2 × √60

From the conversion table the √60 is 7.7459666

√240 = 2 × 7.7459666 = 15.491933

Computing the square root of a prime number is difficult because a prime number is only divisible by itself and one. It involves finding a non-prime number that is less than the prime number and finding a non-prime number that is larger than the prime number: √4 is less than √5 is less than √9 where 5 is a prime number and 2 is less than √5 is less than 3.

(The prime number 5 was chosen because it is a small number. Imagine what it would be like to determine the √313 or other larger prime number!)

From above we know that √4 is less than √5 is less than √9 = 2 is less than √5 is less than 3. Without a square root numbers table we must pick a value between 2 and 3, then multiply the value times itself until the correct answer is discovered.

First determine the square roots of both 9 and 4 then subtract them. Take their difference and divide by 2:

3 − 2 = 1

1 / 2 = .50

Next add the value obtained to the lower non-prime number:

2 + .50 = 2.50

Multiply the result 2.50 times itself:

2.5 × 2.5 = 6.25

The result of 6.25 is greater than 5 so the √5 is less than 2.5 and see that 2 is less than √5 and 2.5 is greater than √5.

The next number to try…

2.5 − 2 = .5 = 1/2

1/2 / 2 = 1/4 = .25

2 + .25 = 2.25

2.25 × 2.25 = 5.0625

It’s getting closer to 5 and see that 2 is less than √5 and 2.25 is greater than √5.

It is easy to see that it can take many attempts to find a number value that when multiplied by itself would equal its original prime square number value.

How to Find the Area of a Square

Square area is one of the most important math measurements. It is a flat surface measurement.

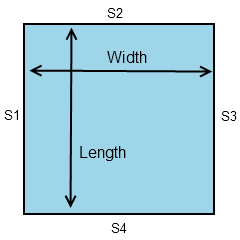
For a square object the length or width of any side is the square root of its area: √A = L or W

To measure the area of a square:

Let A = area, L = length and W = width.

A = L × W where L = W and, L and W are perpendicular.

It means that for any object to be square the width and length must be exactly the same size. If length is one meter then width is one meter, if width is 12 inches then length is 12 inches.

It also means that for any square object the square root of its area is exactly the length or width of that object.

Let S be any side of a square and S1, S2, S3, S4

each represent a unique side:

S1 = S2 = S3 = S4 , and A = L2 = W2 = S2 and √A = L = W = S

Related to area is perimeter. It is the outer boundary of an area. Perimeter is an outline that exactly shows the extent of an area.

Think of perimeter as a fence that completely and exactly surrounds an area. The measured length of the entire fence is its perimeter.

Perimeter, P, of a square is the sum length of its four sides (See diagram above):

P = S1 + S2 + S3 + S4 = 4 × S = 4S

Hypotenuse Formula

The Hypotenuse Formula is C2 = A2 + B2

This formula calculates the length for any side of a right triangle or its hypotenuse.

“C” is the hypotenuse. “A” is the adjacent side and “B” is the opposite side. The intersection of lines A and B form a 90° angle:

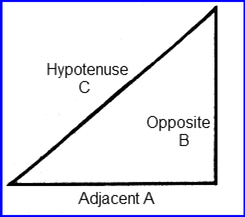
If the adjacent and opposite sides are equal length. The right triangle has an area 1/2 of its corresponding square.

To use the Hypotenuse Formula the lengths for two sides of a right triangle must be known, or the length of any side and the hypotenuse must be known:

C2 = A2 + B2

C = √( A2 + B2)

When:

A = 3, and

B = 4, then

C = 5

C2 = A2 + B2

then,

C2 − A2 = B2

B = √(C2 − A2)

and,

C2 − B2 = A2

A = √(C2 − B2)

The Hypotenuse Formula is commonly known as the Pythagorean Theorem. You may be asking why a theorem for a triangle is included as content about square area and square root math. The answer is simply that the mathematical proof for this theorem is based on analytical geometry involving square area and square roots, and that this theorem is so very important. Please take a few moments to study the following diagram:

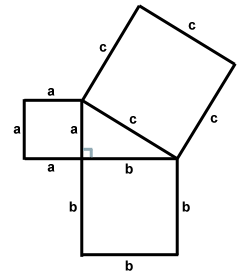
Diagram showing math proof of Pythagorean Theorem using squares and square roots.

Squares have been drawn so that one side of each square is attached to the adjacent, opposite and hypotenuse of the center triangle. Now think about the Hypotenuse Formula given above as C2 = A2 + B2. The area of each square A, B or C is its length multiplied by its width and because A, B and C are each a square their lengths and widths are the same. The area of square A is length A multiplied by width A, and can be written mathematically as A2, the area of square B is length B multiplied by width B, and can be written as B2, the area of square C is length C multiplied by width C, and can be written as C2.

For any values assigned to a side of square A and side of square B their square areas added together (A2 + B2) always equal the area C2, this provides a mathematical proof for the Pythagorean Theorem that

√C2 = √( A2 + B2).

Let opposite A = 3 and adjacent B = 4, for (A2 + B2) = C2

(32 + 42) = (9 + 16) = 25

Since C2 = 25 the √25 = 5 and is the triangle’s hypotenuse length.

Copyright © DigitMath.com

All Rights Reserved.