Mobile Math Website

History of Mathematics
Contributions of Babylonian, Pythagorean and Egyptian Civilizations

Babylonian Mathematics

Our knowledge of Babylonian math is derived from more than 400 clay tablets unearthed since 1850.

Mesopotamian mathematical tablet Plimpton 322, dated to 1800 BC.

Written in Cuneiform script, tablets were inscribed when the clay was moist then baked. Most clay tablets date from 1800 - 1600 BC and include fractions, multiplication tables, algebra, quadratic equations, cubic equations, and reciprocal numerical pairs. Some tablets include methods for solving linear and quadratic equations. The Babylonian tablet YBC 7289, dated 1700 BC, gives an approximation of the square root of two (√2) accurate to five decimal positions.

Babylonian mathematics used a base-60 number system. Our modern day Arabic-based system is base-10 using the digit symbols 0-9.

From the Babylonian base-60 system originates 60 seconds in a minute, 60 minutes in a hour and 360 degrees of a circle,  with each degree divisible into 60 minutes. Babylonian advances in mathematics were assisted by 60 having many divisors. Unlike Egyptians, Greeks and Romans, the Babylonians had a true place-value system, digits written in the left column represented larger values. They lacked an equivalent of a true numeric decimal system, the decimal point for a symbol was implied from the purpose of that numeric symbol.

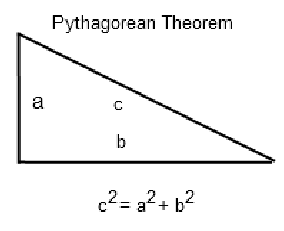
Pythagorean Theorem

Developed after basic arithmetic and geometry the Pythagorean Theorem is the most recognized equation in mathematics history and was known to Chinese and Babylonians more than a millennium before the Greek philosopher, Pythagoras of Samos, 582 - 500 BC. This theorem has captivated humanity for 3000 years. More than 300 mathematical proofs are known today.

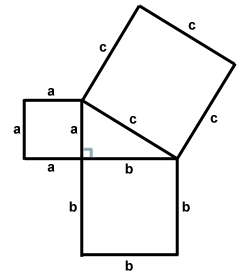
Euclid Diagram

Mathematical Pi (pronounced pie)

The ancient civilizations of Egypt, Babylonia, China and India were interested in evaluating areas or perimeters of circular fields. Pi was not yet a known constant and only implicitly referenced in all discovered historic documents. Perhaps the most famous is the Egyptian Rhind Papyrus which states the rule used to compute the area of a circle: Subtract 1/9th the diameter and take the square of the remainder: pi = (16/9)2.

Archimedes of Syracuse, 287 - 212 BC, Greek Mathematician, Physicist, Engineer, Inventor, and Astronomer developed a method based on inscribed and circumscribed polygons applied primarily until the mid-seventeenth century. It's the first known algorithm to compute pi, in principle, to any required accuracy. In his treatise, Measurement of a Circle, he used regular polygons with 96 sides to show, for any circle, the ratio of the circumference to its diameter is less than 3+1/7, but greater than 3+10/71.

Since the mid-18th century the value of pi has been represented by the Greek letter π.

Egyptian Mathematics

The most extensive Egyptian mathematical text is the Rhind Papyrus, also called the Ahmes Papyrus, dates to 1650 BC.

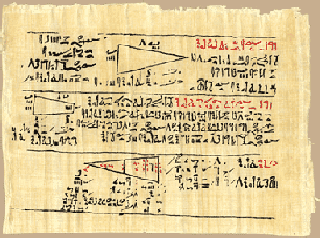
Rhind Papyrus with mathematical pyramid dimensions.

The Rhind Papyrus is an instruction manual for students in Arithmetic and Geometry. The instruction provides formulas for area, methods for multiplication, division and working with unit fractions. It contains evidence of other math knowledge, including composite numbers, prime numbers; arithmetic means, geometric means, harmonic means and perfect number theory, that of the number 6. It shows how to solve first order linear equations, arithmetic and geometric series.

Copyright © DigitMath.com

All Rights Reserved.