Mobile Math Website

Conics and Conic Sections

Conic sections, or simply Conics, were discovered during the Classical Greek Period, 600 - 300 B.C., as geometric properties; the intersections of planes and cones. During the 17th century the purpose of Conics expanded and provided significant insight to the early developments of Calculus mathematics.

Geometric Definition:

A Conic Section is the intersection of a plane and a double-napped cone; the plane that slices the double-napped cone does not pass through the vertex. The result, depending on direction of slice, is a Basic Conic Section shape forming a circle, ellipse, parabola or hyperbola.

Circle:

Conics Circle Slice:

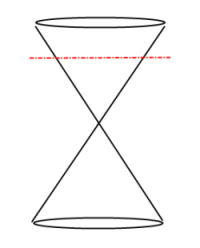
Ellipse:

Conics Ellipse Slice:

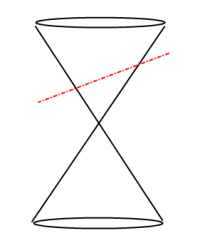
Parabola:

Conics Parabola Slice:

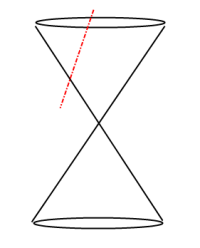
Hyperbola:

Conics Hyperbola Slice:

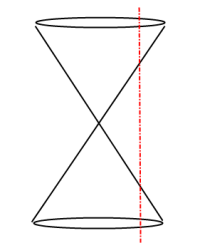
When a plane passes through the vertex of a double-napped cone the result is a Degenerate Conic forming a single point, line or two intersecting lines.

Degenerate Conic forming
 a Single Point:

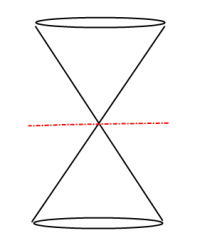
Degenerate Conic forming a Line:

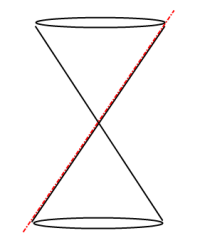
Degenerate Conic forming
Two Intersecting Lines:

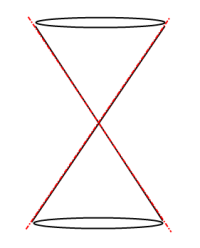
Conics Math Definition:

The algebraic definition of Conics is a general second-degree quadratic equation with two unknown variables x and y. It is from this general math definition that specific definitions for the circle, parabola, ellipse and hyperbola are produced:

Ax2 + Bxy + Cy2 + Dx + Ey + F = 0 when A, B and C are not all zeros.

We will also only consider equations with B = 0, thus eliminating the Bxy term gives us,

Ax2 + Cy2 + Dx + Ey + F = 0

In textbooks and other reference material the Conics general math definition is often written as,

Ax2 + By2 + Cx + Dy + E = 0

It is important to recognize that B is (re)used in the y2 term, the D and E coefficients are respectively replaced by C, D and the constant F is replaced by E.

The Third Approach to Study Conic Sections:

While Conics can be studied from its geometric definition or its general math definition there is a third approach in which each conic section is defined as a locus (collection) of points that satisfy a certain geometric property. Going forward, it is from this perspective that we prefer to define each conic section.

Copyright © DigitMath.com

All Rights Reserved.