Mobile Math Website

Conics Ellipse

The ellipse is similar to a circle. The difference, an ellipse has two axes of symmetry. The longer axis is the major axis and the shorter axis is the minor axis.

An ellipse has two axes of symmetry. This image shows the Ellipse for equation 2x2 + 4y2 = 8:

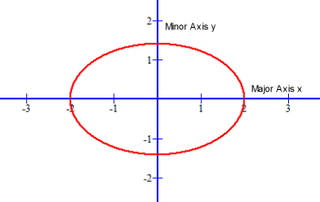
The equation of an ellipse is also similar to the equation for a circle. The graph of x2 + y2 = 25 is a circle and has a coefficient value for each variable that are equal. The graph of 2x2 + 4y2 = 8 is an ellipse, the values of the coefficients of x and y variables are unequal. If the equation has two squared variables of the same sign (positive or negative) with a different coefficient value for each variable, the graph of the equation is an ellipse.

The standard form of the equation of an ellipse with its center at origin and major axis on the x-axis is:

x2 / a2 + y2 / b2 = 1

where a ˃ b

This ellipse has the following properties:

Vertices: (−a, 0) and (a, 0)

Foci: (−√ (a2 − b2), 0) and (√ (a2 − b2), 0)

Center: (0, 0)

Major Axis: x axis (or, y = 0)

Minor Axis: y axis (or, x = 0)

This image is the Standard Form Ellipse Equation
 x2 / a2 + y2 / b2 = 1 when a = 5 and b = 4:

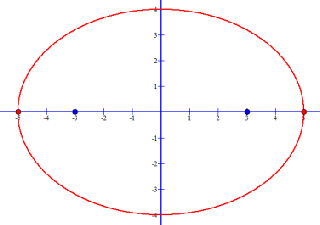
The ellipse with center (0, 0) shows its vertices as red dots and foci as blue dots.

If we interchange the roles of the x and y axis, we obtain the following result:

x2 / b2 + y2 / a2 = 1 where a > b

This ellipse has the following properties:

Vertices: (0, −a) and (0, a)

Foci:  (0, −√ (a2 − b2)) and (0, √ (a2 − b2))

Center:  (0, 0)

Major Axis: y axis (or, x = 0)

Minor Axis: x axis (or, y = 0)

The standard form of the equation of an ellipse with center at (h, k) and major axis parallel to the x-axis is:

(x − h)2 / a2 + (y − k)2 / b2 = 1

If an equation of an ellipse is in standard form and the constant under the (y − k)2 is larger than the constant under (x − h)2 the major axis will be parallel to the y-axis.

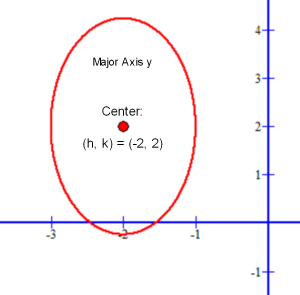
The ellipse equation (x + 2)2 / 1 + (y − 2)2 / 4 = 1.
The constant 4 under (y − 2)2 is greater than the constant 1 under (x + 2)2:

The equation:

Ax2 + Cy2 + Dx + Ey + F = 0

with A and C not equal, but with the same sign, is the general formula of the equation of an ellipse. It is given by the conics general math definition.

Then, by definition, the equation 4x2 + y2 + 16x − 4y + 16 = 0 is an ellipse. This general math form of the equation for an ellipse can be converted to the standard form by completing the squares and dividing both sides of the equation to make the constant on the right side equal to 1:

(4x2 + 16x) + (y2 − 4y) = −16
4(x2 + 4x) + (y2 − 4y) = −16
To complete the squares add 16 to
(x2 + 4x) and
4 to (y2 − 4y), the result gives us …
4(x2 + 4x + 4) + (y2 − 4y + 4) =
                                          −16 + 16 + 4
4(x2 + 4x + 4) + (y2 − 4y + 4) = 4
4(x + 2)2 + (y − 2)2 = 4
Finally, divide both sides of the equation by 4 …
(x + 2)2 / 1 + (y − 2)2 / 4= 1
The ellipse equation is now standard form.

“Once an ellipse equation is standard form it is easiest to determine its vertices, foci, center, major axis and minor axis.”

The ellipse has many practical applications in science and technology: 1) A Planet’s travel is elliptical with one focus being the sun, 2) Elliptical gears, used in power punch and pressing machines, produce a powerful stroke with fast return, 3) Noise control; a whispering gallery room likely has an elliptical ceiling or ceilings arranged so that a noise produced at one focus can only be heard at another focus, between foci noise cannot be heard.

Copyright © DigitMath.com

All Rights Reserved.