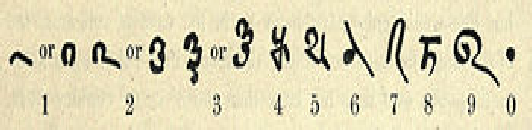History of Mathematics
Contributions of Chinese, Indian and Islamic Civilizations


Chinese Mathematics
The oldest existing work on geometry in China comes from the philosophical Mohist Canons, 330 BC, compiled by the followers of Mozi, 470 - 390 BC. The Mo Jing described various aspects of many fields associated with physical science, and provided a small number of geometrical theorems.
In 212 BC, the Emperor Qin Shi Huang (Shi Huang-ti), Oin Empire, commanded books burned that were not officially sanctioned. The consequence of this order is that little is known about ancient Chinese mathematics before this date. The Han Dynasty, 202 BC - 220 AD, produced works of mathematics which presumably expanded on earlier lost works. The most important is The Nine Chapters on the Mathematical Art. It consists of 246 word problems involving agriculture, business, geometry to figure height spans and dimension ratios for Chinese pagoda towers, engineering and surveying. The Nine Chapters also includes material on right triangles, values of pi, a mathematical proof for the Pythagorean Theorem and a mathematical formula for Gaussian Elimination.
The high-water mark of Chinese mathematics is in the 13th century, latter part of the Sung period, with the development of Chinese algebra. The most important text from that
period is the Precious Mirror of the Four Elements by Chu Shih-chieh and provides the solution of simultaneous higher order algebraic equations using a method similar to Horner's Method. The Precious Mirror contains a diagram of Pascal's Triangle with coefficients of binomial expansions to the eighth power.

Nine Chapters on the Mathematical Art is early surviving mathematical text from China (2nd century AD).
Indian Mathematics
The oldest known mathematical records from India are the Sulba Sutras dated between the 8th century BC and 2nd century AD.
They are appendices to religious texts providing simple rules for constructing altars of various shapes using squares, rectangles and parallelograms.

The numerals used in the Bakhshali Manuscript, dated approximately 200 BC - 200 AD.
As with Egypt, temples connect math and religious ritual. The Sulba Sutras give methods for constructing a circle with about the same area as a given square implying several different approximations of the value of pi. They compute the square root of two having several decimal positions, list Pythagorean Triples, and give a statement of the Pythagorean Theorem. This history strongly suggests a Mesopotamian influence.
In the 7th century, Bramagupta in Brahma-Sphuta-Siddhanta explains the use of zero as a placeholder and decimal digit along with the Hindu-Arabic numeral system. It was from a translation of this Indian text on mathematics, 770 AD, that Islamic mathematicians were introduced to the numeral system they adapted as Arabic numerals. Islamic scholars carried knowledge of this number system to Europe and by the 12th century it replaces other number systems throughout much of the world. In the 10th century Halayudha’s commentary on Pingala’s work contains a study of the Fibonacci Sequence and Pascal's Triangle, and describes the formation of a math matrix.
During the 12th century Bhaskara II lived in southern India writing extensively on all known branches of mathematics. His work contains mathematical objects equivalent or similar to infinitesimals, derivatives, the Mean Value Theorem and the derivative of the sine function. The extent he envisioned calculus is controversial among historians of math.
Progress in mathematics stagnated in India with the establishment of Muslim rule dominant in the 13th - 16th centuries.
Islamic Mathematics
The Islamic Empire established across Persia, the Middle East, Central Asia, North Africa, Iberia, and areas of India in the 8th century made significant contributions to mathematics. Although most Islamic mathematics texts were written in Arabic, the written language of non-Arab scholars, few were written by Arabs.
During the time of the Ottoman Empire and Safavid Empire from the 15th century the development of Islamic math became stagnant.
Copyright © DigitMath.com
All Rights Reserved.